ПриложениеБ

МЕТОД АРИСТАРХА ДЛЯ НАХОЖДЕНИЯ РАЗМЕРОВ СОЛНЦА

На рис. Б.1 показаны геометрические соотношения, необходимые для понимания метода Аристарха, которым он пользовался для нахождения размеров Солнца и Луны [Аристарх, ок. -280]. Горизонтальная прямая, оканчивающаяся справа в точке V, соединяет центры Солнца и Земли. Центр Солнца находится на левом конце этой линии.

 

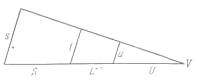Рис. Б.1. Подобные треугольники в конусе тени Земли. Горизонтальная прямая проходит через центры Солнца и Земли; прямая, пересекающаяся с ней в точке V,- касательная к Земле и к Солнцу. Наклонный отрезок в левом углу рисунка - это радиус Солнца, следующий наклонный отрезок - радиус Земли и самый короткий отрезок - радиус тени на расстоянии Луны. Радиус Земли взят равным 1. S -расстояние от Земли до Солнца, L - расстояние от Земли до Луны, U - оставшееся расстояние до вершины тени. Радиусы Солнца и тени равны, соответственно, S и U. Угол с вершиной в точке V сильно увеличен; его истинное значение меньше 1°

 

На расстоянии S от центра Солнца находится центр Земли. Расстояние L равно расстоянию от Земли до Луны (среднему значению этого расстояния), расстояние U - это оставшееся расстояние, до вершины тени точки V. Прямая, пересекающая линию центров в точке V, перпендикулярна сферам Солнца и Земли. Радиус Земли взят равным 1, радиус Солнца равен s. Расстояние и - это радиус тени на расстоянии, равном усредненному значению расстояния до Луны. Символом l я обозначаю радиус Луны, который на рис. Б.1 не изображен.

При определении геометрических соотношений, показанных на рис. Б.1, ни Птолемей (см. раздел VIII.7), ни Аристарх за четыре столетия до Птолемея не использовали простое уравнение (VIII.2), в которое входят угловые величины. Вместо этого они исходили из того, что треугольники на рисунке подобные, и затем приступали к отысканию обозначенных на рисунке расстояний. Если оставить в стороне то, что они исходили из разных данных, то основное различие их методик состоит в следующем: у Птолемея были довольно точные значения необходимых тригонометрических соотношений, а Аристарх мог получить только некоторые пределы, в которых заключены эти соотношения. Хит, следуя статье П. Теннери (я эту статью не смотрел), показывает, как Аристарх мог получить используемые им значения пределов [Хит, 1913, с. 333-336].

Аристарх начинает с формулировки шести предположений (я приводил их в разделе VIII.2). Первые три предположения оправдывают определенные геометрические построения, используемые Аристархом. Повторять их не будем. Четвертое предположение говорит о том, что изображенный на рис. VIII.1 угол D равен 87°; пятое предположение говорит о том, что угол, под которым с Земли видно расстояние и, в два раза больше того угла, под которым с Земли виден радиус Луны l; согласно шестому предположению радиус l виден с Земли под углом 1°.

Затем Аристарх формулирует три главных вывода, которые он доказывает на основании своих предположений. Вскоре я рассмотрю эти доказательства. Потом он доказывает семь теорем, седьмая из которых в нашей терминологии такая:

18 Ð sec 87° Ð 20.                                                                                                   (Б.1)

Предположение 4 я заменю на эту теорему, вернее, я буду пользоваться точным равенством

sec 87°= 19,1073.                                                                                                     (Б.2)

После такой замены из предположений 4, 5 и 6 мы получаем три уравнения, которые я запишу в следующем виде [1]):

l=lL,   u=yL,   S=SL.                                                                                                          (Б.3)

Числовые значения l, y и S получаются из предположений, и несколько позже я их рассмотрю.

На рис. Б.1 изображены три подобных треугольника, и из обычных теорем о подобных треугольниках получаем еще два независимых уравнения:

(U+L)/l = U/u,

(U + L + S)/s = (U+L)/l.                                                                                                        (Б4)

Неизвестное l появляется только в первом из уравнений (Б.З), и мы пока исключим его из рассмотрения. Тогда у нас остается четыре уравнения с пятью неизвестными величинами s, u, S, L и U. Найти пять неизвестных из четырех уравнений невозможно.

Задача не решается, пока мы не получим восьмую теорему Аристарха. Эта теорема говорит о том, что видимые размеры Солнца (угол, под которым оно видно с Земли) такие же, как и видимые размеры Луны. В доказательство этой теоремы Аристарх молчаливо вводит два новых предположения, которые, как он говорит, «очевидны из наблюдения». Эти предположения (я пронумерую их как предположения 7 и 8) такие:

Предположение 7. Луна может полностью закрыть Солнце.

Предположение 8. Продолжительность полного солнечного затмения по времени равна нулю.

Поскольку Луна может полностью закрыть Солнце, то ее видимый диаметр не может быть меньше видимого диаметра Солнца. Поскольку полное затмение не имеет продолжительности, то диаметр Луны не может быть больше диаметра Солнца. Следовательно, видимые диаметры Солнца и Луны равны, и мы получаем соотношение

s=sS.                                                                                                                        (Б.5)

Восьмая теорема Аристарха говорит о том, что s численно равно l из уравнений (Б.3), но сейчас я этим равенством пользоваться не буду.

Теперь мы, по-видимому, можем сделать вывод, что Аристарх обдуманно имеет дело с аппроксимациями. Он предполагает, что имеются единственные значения l, u, L и U, т. е. он отвергает изменение расстояния до Луны. Вполне возможно, как мне кажется, что к тому времени астрономы еще не открыли изменения расстояния. Предположение 7 отрицает кольцеобразные затмения Солнца. Поскольку первая поддающаяся проверке ссылка на кольцеобразное затмение (см. раздел VIII.6) дана почти современником Птолемея, а возможно, такая ссылка была дана и немного позже, то можно предположить, что астрономы времен Аристарха не знали о существовании кольцеобразных затмений. Однако, с моей точки зрения, трудно поверить, чтобы астрономы времен Аристарха считали, что полное затмение заканчивается в один миг и не имеет никакой продолжительности. Сомневаюсь, чтобы наблюдатели, видевшие полное затмение, но не имевшие еще точных единиц измерения времени, склонны были недооценивать продолжительность такого затмения. Напротив, я считаю, что они должны были ее преувеличивать. Поэтому я думаю, что Аристарх вводит предположение 8 для упрощения вычислений, которые иначе были бы очень трудоемкими, если пользоваться имевшимися в то время методами [2]).

Интересна также ошибка Аристарха, допущенная в предположении 6. Но прежде чем перейти к ее обсуждению, давайте закончим рассмотрение рис. Б.1. Аристарху была недоступна большая часть математического аппарата, который мы считаем очевидным, поэтому его метод кажется нам громоздким. И вместо его способа я приведу простой способ решения. Сперва с помощью уравнений u=yL и s=sS исключим u и s; затем исключим S, используя соотношение S=SL. Итак, у нас осталось два уравнения с двумя неизвестными

U + L = U/yL,

U + L = (U/sSL) + (l + S)/sS.                                                                                             (Б.6)

Неизвестные U и L появляются теперь только в выражениях (U + L) и U/L, так что в данный момент именно эти выражения мы и должны рассматривать как неизвестные. Нетрудно найти, что

U/yL = U + L = (1 + S)/(sS -y).

Поскольку во второе из уравнений (Б.4) входит только выражение U + L, то мы можем сразу решить это уравнение относительно S и, следовательно, определить s, L и /. Результаты такие:

S = (l + S)/(s+ y),        L = (l + S)/S(s + y),

S = (l + S)/[l+(y/s)],     l = [(l + S)/S][l/(s + y)].                                                               (Б.7)

Оба радиуса и оба расстояния зависят от S. Кроме того, расстояния зависят от s и y, а радиусы от этих величин не зависят. Радиус s зависит от отношения y/s, а не от какого-либо из значений y или s в отдельности. Радиус l зависит от отношения l, к s+y и также не зависит от значений самих этих величин. Аристарх предполагает, что значения l и s равны и что значение y в два раза больше любого из них. Если мы подставим эти соотношения в уравнения (Б.7), то окончательно получим следующее:

S = (l+S)/3s,   L = (l+S)/3Sl,

s = (l+S)/3,       l = (1+S)/3S.                                                                                    (Б.8)

Если взять S равное sec 87° и использовать равенство (Б.2), то получим, что значение s равно 6,702 радиуса Земли. Куб этого числа дает нам отношение объемов, и оно больше 300. Значение l равно 0,3508 радиуса Земли и отношение объемов равно 0,0432. Эти значения, как я уже говорил, не зависят от s или l. Расстояния S и L оказываются равными, соответственно, 384,040 и 20,099. Такие результаты получаем, если считать, что видимые диаметры Солнца или Луны равны 2°. Значение L, очевидно, получилось слишком маленьким. Однако если взять видимые диаметры равными 30' (а по словам Архимеда [Архимед, ок.- 225] именно такое значение на самом деле нашел Аристарх), то значения S и L получаются почти точно в четыре раза больше. Новое значение L вполне приемлемо, хотя в этом случае оно получается немного больше чем надо.

В основном Аристарх интересовался размерами (объемами) Солнца и Луны, которые не зависят от значения, использованного для видимого диаметра Луны. Основные выводы Аристарх формулирует сразу после предположений, и они имеют отношение только к размерам. Кроме того, его ошибочное предположение о размерах видимого диаметра Луны не влияет на справедливость ни одной из сформулированных им промежуточных теорем. Видимый диаметр он использует только для доказательства определенных утверждений, которые мы, возможно, приняли бы как очевидные, но которые в его время составляли предмет некоторой задачи.

Для того чтобы понять стоящую перед Аристархом задачу, посмотрим на расположение Солнца, Земли и Луны, показанное на рис. Б.2. Конфигурация такая, что прямые из центра Луны М до центра Солнца S и до центра Земли Е пересекаются под прямым углом. Аристарх считал, что угол D равен 87°. Плоскость, проходящая через точку М и перпендикулярная прямой MS, проходит также и через точку Е.

Поскольку Солнце больше Луны, то плоскость, делящая Луну на светлую и темную стороны, не проходит через точку М. Эта плоскость на рисунке расположена слева от точки М. Аристарх хочет доказать, что этим можно пренебречь и считать, что «разделяющая» плоскость проходит через точку М. Для этого ему надо найти верхние пределы для значений двух величин - расстояния между двумя плоскостями и разности радиусов тех кругов, по которым эти плоскости пересекают сферу Луны. Затем Аристарх показывает, что можно пренебречь значениями, полученными для верхних пределов, а значит, а fortiori [3]) можно пренебречь и действительными значениями этих величин.

Аристарх пользуется размерами видимого диаметра Луны только для определения упомянутых верхних пределов. Он брал видимый диаметр Луны равным 2°, и получившиеся в этом случае пределы больше тех значений, которые соответствовали бы видимому диаметру Луны, равному 30', хотя из рис. Б.2 это, возможно, и не очевидно. Так что используя большие чем надо значения, Аристарх усиливает свои доказательства. Именно это, как я считаю, послужило причиной тому, что в своем сочинении о размерах Солнца Аристарх берет видимый диаметр Луны равным 2°. Это вовсе не то же самое, что использование некоторого значения для иллюстрации. Это хорошо известный прием использования заведомо преувеличенных значений для усиления доказательства.

Аристарх использует аппроксимацию для некоторых других величин, помимо видимых размеров Луны. Другие аппроксимации довольно точные, особенно если он собирался применять их в качестве средних значений.

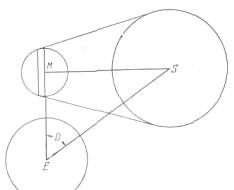
Рис. Б.2. Расположение Солнца,  Земли и, Луны, когда их центры образуют прямоугольный  треугольник. Поскольку Солнце больше Луны, то освещено  больше половины Луны,   как и показано на рисунке