Г л а в а VI

ДОЛГОТА  ПОЛНОЙ  ЛУНЫ

 

1. Параллакс

 

Параллакс - это угол между направлениями, по которым объект виден из двух разных точек. В астрономии почти всегда одна точка - центр Земли, а вторая - точка на поверхности Земли, в которой проводятся астрономические наблюдения [1]). Если расстояние до на­блюдаемого объекта велико по сравнению с размерами Земли, то па­раллакс будет, очевидно, маленьким. Поэтому при наблюдениях невооруженным глазом параллаксами Солнца, планет и звезд можно пренебречь. Но Луна достаточно близка к Земле, и в теории Луны мы должны с самого начала учитывать ее параллакс [2]).

В общих чертах явление параллакса проиллюстрировано на рис. VI.1. Пусть задана система координат XYZ. Ось X - направление на весеннее равноденствие из центра Земли. Оси Y и Z определим позже. Точка Т - это положение наблюдателя на поверхности Земли. Рас­стояние СТ берем равным единице. Положение наблюдателя Т опреде­ляется с помощью двух угловых координат. Для нахождения этих координат проведем плоскость через точку Т (положение наблюдателя) и ось Z. Данная плоскость проходит через прямую ZC, точку Т и точ­ку, обозначенную на рисунке как Т'. Одна координата - это угол ТСТ', другая -угол Т'СХ.

Для точки Р мы можем ввести углы, аналогичные углам ТСТ' и Т'СХ. На рис. VI.1 это были бы углы РСР' и Р'СХ. Если точка Z - Северный полюс, а плоскость XY - экваториальная плоскость, то угол РСР' называется склонением, угол Р'СХ - прямым восхожде­нием. Склонение аналогично широте, а прямое восхождение-долготе. Если плоскость XY - плоскость эклиптики, то угол РСР' называется эклиптической широтой, а угол Р'СХ - эклиптической долготой [3]). Мы можем рассмотреть систему координат с осями, параллельными X, Y, Z, но с началом в точке Т. Координаты в такой системе назы­ваются топоцентрическими, а в системе координат с началом в точке С- геоцентрическими. При выводе или табулировании эфемерид небесного тела желательно, чтобы эфемериды не зависели от точки на поверх­ности Земли. Поэтому предпочтительнее давать эфемериды в геоцент­рических, а не в топоцентрических координатах. Но из наблюдений мы получаем именно топоцентрические координаты, и мы должны уметь от этих координат переходить к геоцентрическим.

В большинстве случаев оба геоцентрических угла отличаются от соответствующих топоцентрических углов. Поэтому у нас может быть параллакс по склонению, прямому восхождению, эклиптической ши­роте и эклиптической долготе. Другими словами, говоря о параллаксе, необходимо точно определять, к какой координате он относится.

 

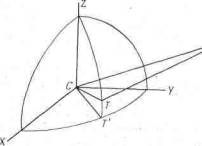Рис VI.1. Астрономический параллакс Точка С - центр Земли, точка Т - положение наблюдателя на поверхности Земли Плоскость, проходящая через точку Т и ось CZ, пересекает плоскость XY по прямой СТ'. Угловое положение точки Т определяется координатными углами ХСТ' и ТСТ Угловое положе­ние внешней точки Р определяется на­хождением точки Р' и заданием коор­динатных углов ХСР' и РСР' (точки Р' на рисунке нет). Предположим, мы ввели другую систему координат с нача­лом в точке Т и определили положение точки Р в новой системе координат ана­логичными построениями Если только Т не находится на прямой СР, то координат­ные углы с вершиной в точке Т отличаются от углов с вершиной в точке С. Это и есть явление параллакса.

 

Через точки С, Т и Р всегда можно провести плоскость, и в неко­торых случаях нас интересует параллакс только в этой плоскости. Ясно, что по перпендикулярному к этой плоскости направлению параллакса нет. Такая ситуация показана на рис. VI.2. На этом ри­сунке плоскость X'Y' - это плоскость, проходящая через точки С, Т и Р. В этой плоскости у нас только одна угловая координата. Угол PCX' - геоцентрический координатный угол λ точки Р. Угол λ_Т- соответствующий топоцентрический координатный угол точки Р. И наконец, координатный угол λ₀(угол ТСХ') определяет положение точки Т относительно точки С. Расстояние СР обозначаем R, радиус СТ равен 1.

На плоскости параллакс можно описать достаточно простыми соот­ношениями. У точек Т и Р прямоугольные геоцентрические координаты (Х'_Т,   Y'_T) и   (X'_Р, Y'_Р) такие:

Х'_Т =cos λ₀,     Y'_T = sin λ₀;    X'_P = R cos λ,   Y'_P = R sin λ.

Следовательно, если смотреть из точки Т, то одна координата точки Р равна R cos λ-cos λ₀, вторая равна R sin λ-sin λ₀. Угол λ_Т можно найти   из   уравнения

tg λ_Т =(R sin λ_Т-sin λ₀)/(R cos λ - cos λ₀).

Мы должны найти разность между углами λ_Т и λ. Используя тригонометрическое выражение tg(A-B) через tg А и tg В, легко по­лучаем

tg(λ_Т - λ) = sin(λ_Т- λ₀)/[R-cos(λ_Т- λ₀)].          (VI.1)

Уравнение (VI.1) я написал, чтобы явно указать зависимость паралла­кса λ_Т - λ_Т от R и от разности направлений λ- λ₀ (разность геоцентри­ческих направлений наблюдаемой точки Р и положения наблюдателя  Т). Аналогичное уравнение мы можем получить   и в   общем случае (рис. VI. 1). Правда, здесь вывод значительно более трудоемкий. Об­щий случай мы не используем, и результаты я не  привожу [4]).

Хотелось бы знать, какое максимальное значение может принимать параллакс. Максимум будет в том случае, если прямые СТ и ТР (рис. VI.2) перпендикулярны, т. е. если прямая от объекта до Земли является касательной к Земле. А значит, в случае максимального па­раллакса прямая ТР - горизонтальная линия. Поэтому и максималь­ное значение часто называется горизонтальным параллаксом. Макси­мальное значение параллакса будем обозначать символом П. Нетрудно получить соотношение

sin П=l/R.      (VI.2)

 Если расстояние R большое, то синус и сам угол (измеренный в ради­анах) равны, т. е. для больших R

П=1/R.       (VI.3)

 

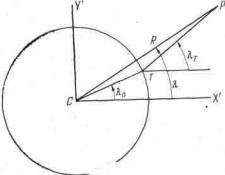
Рис. VI.2.    Частный    случай    парал­лакса (на плоскости)   Рисунок  лежит в плоскости,  проходящей через точки С, Р и Т рисунка VI.1, X' и   Y' - ко­ординатные  оси    на   этой   плоскости. Угол λ- это  координатный угол точ­ки  Р относительно точки С,   а   угол λ_Т - относительно точки Т. Угол λ₀ - координатный угол наблюдателя Т от­носительно  точки С   В   данном   час­тном случае параллакс равен разности λ_Т - λ_.   Эта   разность    равна     углу СРТ, т.   е. параллакс точки Р равен угловому расстоянию между  точками С   и   Т,    если смотреть   из   внешней точки Р.

 

Итак, нахождение горизонтального параллакса П эквивалентно на­хождению расстояния R.

Если R около 60 (как, например, для Луны), то уравнение (VI.3) не достаточно точно, и мы должны использовать уравнение (VI.2). Для очень точных телескопических наблюдений уравнение (VI.3) не подходит, в остальных же случаях (для Солнца и планет) мы можем им пользоваться.

В разделе IV.7 я мельком уже упоминал о параллаксе звезд. Коли­чественные выражения параллаксов звезд нам не потребуются, однако желательно сказать еще несколько слов, чтобы исключить неверное понимание. В уравнении (VI.3) единица в числителе - это радиус Земли, т. е. расстояние от наблюдателя до центра Земли. Если рас­сматривать звезды, то это расстояние ничтожно мало по сравнению с расстоянием до звезды. Пусть на рис. VI.2 точка С - это Солнце, Т - Земля, а круг с центром в точке С - орбита Земли. По мере дви­жения Т по своей орбите в течении года можно наблюдать параллакс звезд) [5]). Максимальный параллакс данной звезды задается уравнени­ем (VI.3), но здесь единица в числителе - это средний радиус орбиты Земли, а эта величина примерно в 23 000 раз больше радиуса земного шара. Но даже в этом случае наибольший известный нам па­раллакс звезды меньше 1". Значит, расстояние до ближайшей звезды более чем в 200 000 раз превосходит радиус орбиты Земли.