6. Точность модели движения Луны по долготе

 

Модель движения Луны, изображенная на рис. VII.2, дает нам способ вычисления и долготы Луны, и расстояния до нее от Земли. В разделе VIII.5 я рассмотрю точность, с какой по этой модели можно определять расстояние. Сейчас же я рассмотрю точность модели только по долготе Луны.

Изучив птолемеевы модели для Солнца, Луны и планет, Дрейер пишет: «Почти во всех деталях (кроме изменения расстояния до Лу­ны) [1]) модель геометрически представляет движения настолько хорошо, насколько это возможно, если пользоваться простыми приборами...» [см. Дрейер, 1905, с. 200]. Многие авторы после Дрейера и, возможно, многие до него придерживались такого мнения. Я же при детальном изучении моделей Птолемея не нашел никаких обоснований подобным утверждениям. Думаю, что это иллюстрация хорошо известного прин­ципа, который можно назвать «увековечиванием ошибки».

Этот принцип можно сформулировать следующим образом. Пред­положим, что ошибка, сделанная автором А, была как-то опубликова­на. И пусть более поздний автор Б цитирует или упоминает эту ошибку, принимая ее за истинное утверждение. Вот ошибка и ста­новится вечной и искоренить ее из научной литературы уже нельзя. Конечно, нельзя серьезно говорить о том, что исключений не бывает. Однако имеется поразительно много примеров, для которых этот принцип верен. Каждый читатель, наверное, сможет привести свои примеры.

Чтобы оценить точность лунной модели Птолемея, я сначала вы­числил долготу Луны по теории Брауна [2]) для 51 момента времени с промежутком, равным 139 суткам. Полученные данные соответство­вали интервалу времени примерно в 19 лет. В конце этого периода Солнце и Луна довольно близко подошли к тем положениям, какие они занимали в начале. Потом я написал программу вычисления ее поло­жений непосредственно по теории Птолемея на те же самые моменты времени и сравнил результаты, полученные но двум теориям. У Пто­лемея были ошибки в значениях n₍ и γ′₍ так что сравнение зависит и от усредненной эпохи. Чтобы обойти эту трудность, я сделал значение усредненной долготы одинаковой. Для этого ко всем долготам, полу­ченным по теории Брауна, я прибавил константу. Проведя такое сравнение, я стал менять в теории Птолемея параметры до тех пор, пока не получил результаты, наиболее близкие к результатам, получившим­ся по теории Брауна. В процессе таких изменений значения n₍ и γ′₍ оставались постоянными, а менял я значения L₀ и γ₀  в начальную эпоху, радиус эпицикла r и расстояния ЕС₁ и EС₂ (см. рис. VII.2) [3]). Эти расстояния я обозначаю соответственно ρ₁ и ρ₂.

Таблица  VII.2

Сравнение птолемеевых параметров для Луны с «наиболее подходящими»

Сравнение полученных результатов легко провести с помощью таблицы VII.2. В первыхпяти строках таблицы приведены значения Птолемея и «самые подходящие» значения пяти параметров L₀, γ_0, r, ρ₁ и ρ₂. Единицей расстояния в этом случае служит радиус дефе­рента для Луны, находящейся в си­зигии. В таком масштабе расстоя­ние Р (рис. VII.2) равно 1- ρ₁. Следующие две строки дают зна­чения, получившиеся для E₁ и E₂. Величина E₁- это максимальное значение уравнения центра для Лу­ны, находящейся в сизигии, а E₂ - максимальное значение уравнения центра Луны в фазе четверти, В по­следней строке таблицы даны значе­ния а, среднего квадратичного от­клонения погрешности.

Максимальная погрешность, по­лученная с параметрами Птолемея, равна 1,08°, а среднее квадратичное отклонение равно 0,581°, около 35'. Видимый диаметр Луны, находящей­ся на среднем расстоянии от Земли, примерно 33', так что ошибка в несколько раз больше видимых разме­ров Луны. Мне кажется, подобную теорию нельзя считать большим достижением. Вне всякого сомнения, она не дает долготу с той точ­ностью, какая достигалась в астрономических наблюдениях греков. Мы видим, что дело здесь не в неудачном выборе параметров; сама модель не такая уж удачная. Даже для «наилучшего» выбора параметров среднее квадратичное отклонение уменьшается только до 0,558 (около 33 1/2 минуты дуги).

В книге Теннери [1893, с. 211 и далее] показано, что в модели Птолемея есть и эффект эвекции, и она отражает примерно половину того эффекта, который в уравнении (VI.4) описывает член, названный вариацией. Соответствующее выражение равно 0,66°sin 2D, где D - элонгация Луны. На основании этого в Части I я написал, что модель Птолемея описывает эвекцию, а также «частично согласуется» с ва­риацией [4]). Но тщательно изучив ситуацию, я понял, что это утвержде­ние неверно. В подтверждение приведу два соображения.

Сначала из модели Птолемея Теннери получает формальное выра­жение для уравнения центра и дает это выражение в форме ряда по степеням расстояний r и ρ. В разложении есть члены, соответствую­щие членам 6,29° sin M, 0,22° sin 2M и 1,27° sin(2D-M) из уравнения (VI.4), но коэффициенты получаются несколько другими. В обозначениях, использовавшихся в этой книге, оставшиеся в разложении члены с точностью до числового коэффициента равны

sin 2D [cos(2D + M)+ 2 cos(2D-M)].

Коэффициент равен примерно 0,30°. Если умножить этот коэффициент на максимум выражения в квадратных скобках, то получим 0,53°, зна­чение, довольно близкое к коэффициенту 0,66° в вариации. Эту вели­чину надо умножать на sin 2D, как в вариации, поэтому Теннери и гово­рит, что такое выражение соответствует определенной части вариации.

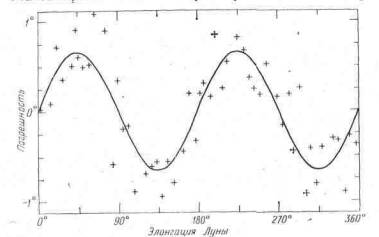
Рис. VII.6. Ошибка в птолемеевой модели движения Луны, представленная как функция элонгации Луны. Ошибка вычислялась так: из значения, полученного по теории Брауна, вычитали значение, полученное по теории Птолемея. Знаками «+» отмечены ошибки, вычисленные для 51 момента времени с интервалами в 139 суток между ними Кривая - это функция 0°,66 sin 2D, где D - элонгация.

 

Теннери не исследует ситуацию достаточно глубоко, и это объяс­няется, возможно, тем, что затронутый вопрос не очень важен. А ведь он мог увидеть, что величина в квадратных скобках для каждого значения D, если взять усреднение по аномалии М, в среднем равна нулю. Поэтому этот член в выражении, найденном Теннери, вовсе не соответствует вариации; он просто показывает, насколько модель Птолемея расходится с эвекцией [5]).

Теперь давайте рассмотрим погрешность в модели Птолемея для отдельных моментов времени. На рис. VII.6 по оси к отложена элон­гация D, по оси у отложены погрешности. Знаками «+» отмечена 51 по­грешность для отдельных моментов времени, кривая - это функция 0,66° sin 2D. Кривая довольно хорошо вписывается в отмеченные зна­ками «+» отдельные погрешности. Другими словами, похоже, что погрешности равны вариации 0,66° sin 2D и еще различным малым воздействиям, зависящим от других величин. Непохоже, чтобы модель описывала какую-нибудь часть вариации.

Но тогда перед нами встают другие вопросы. Мы предполагаем, что радиус деферента в квадратурах меньше, чем в сизигиях, и, таким образом, можно получить достаточную точность для уравнения центра в этих фазах. Почему же Птолемей делает поправку для октантов (в этих фазах элонгация равна нечетному кратному 45°)? Как случилось, что решив сделать такую поправку, Птолемей выбрал то значение параметра ρ₂, которое удивительно близко к значению, обусловленному эвекцией? Последний вопрос требует некоторого пояснения.

Заменим в уравнении VI.4 значения М (измеренные от перигея) на γ+180°, где γ измеряется от апогея, и оставим только два старших члена. Тогда

е_C=-6,29° sin γ-1,27° sin (2D-M).

Пусть, например, D=45° (любое другое нечетное кратное 45° даст аналогичный результат). В этом случае получаем:

е_C=-6,29° sin γ-1,27° cos γ.

Если 7=0, то е_C=-1,27°. Это, в свою очередь, позволяет нам опреде­лить на рис. VII.5 точку K, от которой надо измерять аномалию, если модель правильно дает эвекцию. В результате получаем, что для D=45° угол между Z и К. равен 13,1°. По таблицам Птолемея этот угол равен 12,0°.

Но для других значений D по таблицам Птолемея нельзя получить такие хорошие результаты. Например, для D=60° мы получаем, что е_C=-1,10°, если γ=0. Используя соответствующий D=60° радиус деферента, находим, что угол от Z до К уменьшается до 10,3°, а по таблицам Птолемея он увеличивается до 13;04=13,07 градуса.

Если оставить в стороне последний из рассмотренных вопросов, то у Птолемея, видимо, не было оснований для предположения о том, что эвекция может быть выражена с помощью члена, пропорционального sin(2D-γ), и поэтому он, вероятно, не мог использовать приведенные аргументы. Но если проведенное Гиппархом 2 мая -126 г. измерение было подлинным до того, как Птолемей изменил его своей подделкой, то Птолемей должен был увидеть, что с его моделью для D=315° не все благополучно. В этот момент по вычислениям Птолемея у была рав­на 185;30 градуса, а это приводит к е_C=+0,665° (почти точно 0;40). Но правильное значение уравнения центра на этот момент было равно -1;22 градуса, и подлинное наблюдение привело бы к очень близкому значению. Следовательно, надо довольно сильно изменять аномалию; модель Птолемея дает для этого наблюдения значение е_C=-0;46,

С наблюдением 7 июля-126 г. дело обстоит несколько иначе. У Птолемея γ равнялась 333;12 градуса; такому значению у соответ­ствует е_C=2;32 градуса. Это очень близко к верному значению 2;19 гра­дуса. Так что значительных изменений аномалии не требуется. В среднем же изменение, получающееся по обоим наблюдениям, довольно близко к той величине, какую брал Птолемей.

Для своей окончательной модели Птолемей так подгоняет данные, чтобы ρ₁ и ρ₂ были равны. Я не думаю, чтобы к этому равенству Птолемей пришел в результате усреднения по большому количеству результатов. С одной стороны, если бы он так поступил, то получил бы изменение, соответствующее D=45°, близкое к 13,1°. С другой стороны, Птолемей часто так подгоняет данные, чтобы какой-нибудь важный параметр был равен целому числу, либо чтобы два параметра получи­лись равными. В разделе VI.7 мы рассматривали, как Птолемей нахо­дит максимальное значение уравнения центра в сизигиях, и это почти наверное является примером подделки первого типа. В дальнейшем мы получим примеры подделок второго типа. Я думаю, Птолемей просто взял ρ₂ равным ρ₁; равенства он любил.

Но есть еще один вопрос, который я до сих пор не рассматривал. Почему у Птолемея максимальное значение уравнения центра для Луны в квадратуре равно 7;40? В Части I (тогда я еще не обнаружил просчетов в его вычислениях) я верил словам Птолемея о том, что к значению 7;40 градуса приводит наблюдение Гиппарха от 5 августа -127 г. Теперь мы знаем, что из наблюдения Гиппарха такое значение не получается, и следовательно, мы должны спросить: откуда Птолемей берет это значение? Вопрос тем более уместен, что, как мы знаем, Пто­лемей, чтобы получить значение 7;40, сфабриковал и свое наблюдение, и наблюдение, приписанное им Гиппарху.

Удовлетворительного ответа на этот вопрос я не нашел. Не думаю, что Птолемей выбрал 7;40 градуса на основе «магии чисел». Но здесь может быть причина, о которой я не знаю. Возможно, конечно, что Гиппарх оставил большое количество наблюдений, по которым в сред­нем получается значение 7;40 градуса. Погрешность в таком значении составляет около 0,11°. Вариация с ее самым большим коэффициентом 0,66° не влияет на показания приборов в квадратурах, поэтому до­статочное число достаточно аккуратно проведенных наблюдений, могло бы привести к среднему значению, имевшему подобную точ­ность.

На рис. IV.5 показана модель, которую я назвал моделью вторич­ного эпицикла. В основе этой модели лежит изменение r, расстояния от  до Луны, а не радиуса деферента R. Если мы применим такую модель к Луне, то получим модель, показанную на рис. VII.7. Угол, E^ - это средняя долгота Луны. У первого эпицикла (с центром в точке ) радиус MB направлен на положение апогея Луны. Этот ра­диус вращается с периодом, равным 8,85 года. Угол ВМ равен 2D; точка М обозначает положение Луны. Радиус первого эпицикла выбран так, чтобы максимальное значение уравнения центра было равно 6,29˚. Радиус второго эпицикла выбран так, чтобы это значение изменилось на величину 1,27°, если оба радиуса расположатся вдоль одной прямой.

Среднее квадратичное отклонение погрешности этой модели состав­ляет 0,545°. Таблица VII.2 показывает, что модель вторичного эпи­цикла немного точнее модели Птолемея, независимо от того, брали ли мы последнюю с параметрами Птолемея, или же с «наиболее подхо­дящими» параметрами. Однако значительное преимущество модели вторичного эпицикла не в этом. Два основных преимущества модели вторичного эпицикла в другом. Первое состоит в том, что эта модель намного лучше представляет расстояние до Луны, чем модель Птоле­мея (это мы увидим в следующей главе). Второе преимущество со­стоит в том, что модель вторичного эпицикла дает, по существу, ту же точность по долготе, что и модель Птолемея, но модель вторичного эпицикла намного проще. С этой моделью астрономам было бы намно­го легче открыть систематическое расхождение, называемое вариа­цией. А так вариация не была открыта примерно до 1600 г. Кроме того, модель можно изменить так, чтобы учесть вариацию. И полу­чающаяся окончательная модель, хотя и значительно более точная, все же была бы не сложнее модели Птолемея.

В главе IV.6 я говорил, что первым из европейских ученых исполь­зовал модель вторичного эпицикла для Луны Коперник [Коперник, 1543, глава IV.3]. Но такой моделью за два столетия до Коперника поль­зовался мусульманский астроном ибн аш-Шатир [Нейгебауер, 1968, с. 191-192]. Мы не знаем, изобрел ли Коперник эту модель независимо или нет.

 

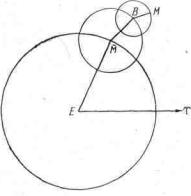Рис VII.7. Модель вторичного эпи­цикла для Луны. Точка Е - Зем­ля, прямая Е^ направлена на точ­ку весеннего равноденствия Точка М - Луна, а  - средняя Луна. Таким образом, угол ^ равен средней долготе Луны Прямая от М к В направлена на апогей Луны, угол ВМ равен удвоенной элон­гации Луны. Прямая ВМ вращает­ся против часовой стрелки. Если расстояние Е взято равным еди­нице, то радиусы эпициклов равны 0,109801 и 0,022 164

 

 

 

 

Я также рассчитал точность, какая получается при использовании одного эпицикла с таким радиусом, чтобы максимальное значение уравнения центра было равно 6,29°. Среднее квадратичное отклонение равно 1,094°, примерно в два раза больше, чем для модели Птолемея или для модели вторичного эпицикла. Модель Птолемея, конечно, больше подходит для описания геоцентрической долготы Луны, чем модель с одним эпициклом. По сравнению с такой моделью погрешность по долготе в модели Птолемея вдвое меньше. Более того, в модели Пто­лемея проявляется систематическое различие между фазами сизигий и квадратур. Это улучшение получено ценой значительной потери точ­ности описания расстояния до Луны (это мы увидим в следующей главе).

Большая ошибка при определении расстояния до Луны означает большую ошибку при определении параллакса, который входит в топоцентрическую долготу. А ведь именно эту величину в действи­тельности наблюдают астрономы. Поэтому неясно, дает ли модель Птолемея какое-либо улучшение для определения наблюдаемой дол­готы. Мне кажется, что по обычным нормам оценки научного дости­жения в общем модель Птолемея надо считать неудачной.